Firm Learning and Market Equilibrium
One goal of the field of industrial organization is to predict the response of markets to environmental or policy changes. A market, for our purposes, is a collection of firms that produce and sell competing products or services. Since the consequence of, say, a price change by a given firm depends on the prices of competing firms, realism requires analyzing these changes in the interacting agent frameworks supplied to us by our game theory colleagues. If a firm had set a profit maximizing price before an environmental change, that price was unlikely to be optimal after, say, a tariff or merger induced a price change by a competitor. It is important to take account of the price adjustments that followed the initial price change.
An explicit model of firm behavior might let the price change by firm A lead to a response by firm B, which would lead to a further price change from firm A, and so on. Rather than following this modelling strategy, a substantial body of applied work focuses on finding the Nash equilibrium after an environmental change. There is an intuitive appeal to proceeding in this way. Sticking with the pricing example, in a Nash equilibrium each firm's price maximizes its own profits given the prices of every other firm. So as long as firms are trying to maximize profits, the Nash equilibrium will constitute a "rest point" to any model of how the responses to the change actually occur. In a Nash equilibrium, no firm has an incentive to change its price (to "deviate"), and away from such an equilibrium at least one firm has an incentive to change its price, so further changes are likely to occur.
My research, spanning several decades, has focused on the use of the Nash equilibrium concept in empirical research and the estimation of demand and production functions that are key inputs to firm behavior. Early contributions on estimating demand functions with Steven Berry and James Levinsohn1, on estimating production functions with G. Steven Olley2, and on the use of Nash equilibrium in dynamic contexts with Richard Ericson3, led to shifts in the paradigms used to analyze price and productivity responses to environmental change. However, when the concept of Nash equilibrium was extended to analyze investment responses, the cognitive requirements of both agents and researchers seemed unrealistic.4 This led Chaim Fershtman and me to consider how firms learn to achieve their goals.5
Understanding the learning process has two further advantages. First, it takes time to get from one equilibrium to another, and if we only analyze equilibria, we give up on investigating how long that takes and what is likely to happen in the interim. There is also a more subtle point: In many situations there can be more than one Nash equilibrium. If firm A chooses x it may well be an equilibrium for firm B to choose x' while if firm A had chosen y, which differs from x, we would expect that firm B 's equilibrium response would differ from x' Since the different equilibria can have different properties, this not only impacts our ability to predict the implications of a given environmental change, but also impacts the desirability of the change. A realistic model of how firms react to changes would not only provide information on the transition path to a new equilibrium, but might also indicate which equilibria are more likely to occur.
My recent research with Ulrich Doraszelski and Gregory Lewis examines the process by which firms learn.6 We follow the sequence of events in the electricity market for frequency response (FR) in the United Kingdom immediately after deregulation. We investigate how firms react to the change with an eye to formulating a framework for analyzing behavioral responses to change in the economic environment.
FR is a product needed to keep the electricity grid running in the face of shocks to demand or supply that could not be predicted when the auction designed to clear the market occurred. FR gives the operator/owner of the electricity grid (National Grid) the ability to take over generators and change the power they generate to ensure that the frequency in the wires that transport the electricity stays within a safe range specified by a regulator.
Historically, electricity-generating firms had been required to provide FR to National Grid at a fixed price. On November 1, 2005 the market for FR was deregulated, and we follow the market for six years from that date. In the deregulated market, firms submit bids for each of their generators during the month prior to the month where it is relevant. Firms own stations and stations contain several generators of the same type and vintage. If called upon, the generator gets paid a holding payment equal to its bid times the quantity of electricity (in megawatt hours) that the operator can access, and the operator has the right to take over the generator when it wishes. There is also an adjustment made to compensate the generator for changes in the energy cost of running the generator when it is called for FR. A supercomputer running a proprietary program chooses generators to supply FR to minimize the cost of FR to the operator subject to the legal requirements for FR and various technological constraints.
All market participants in the first 3½ years post-deregulation had been active prior to deregulation and were familiar with demand conditions. Also, cost conditions were relatively stable over this period. For the latter part of our sample there was some entry, and more substantial changes in both factor costs and in market institutions. As a result, the initial bid changes can largely be attributed to firms learning how to adapt to the new rules, though later on we expect to see responses to further environmental changes.
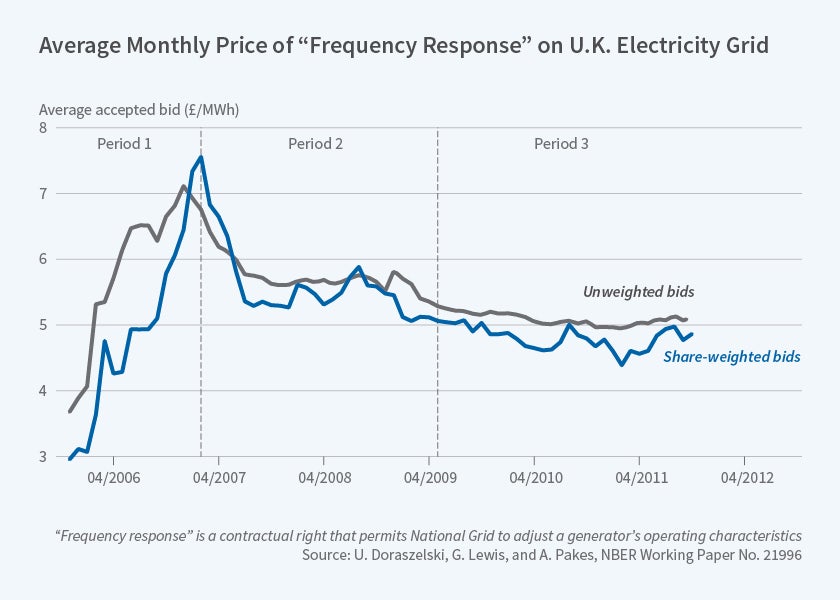
There was a lot to learn. Initially firms did not know how their competitors were likely to bid, nor did they know how the computer program would respond to the changes in their bids given their competitors' bids. We focus on the behavior of the 10 largest firms that, as a group, accounted for about 85 percent of the revenue generated by the FR market during our sample period. Figure 1 provides the share-weighted and simple averages of the bids. The dotted lines separate three periods. The first period sees climbing prices, the second sees falling prices, and in the third period, the period that hosted changes in the underlying market conditions, prices appeared to stay within a narrow range.
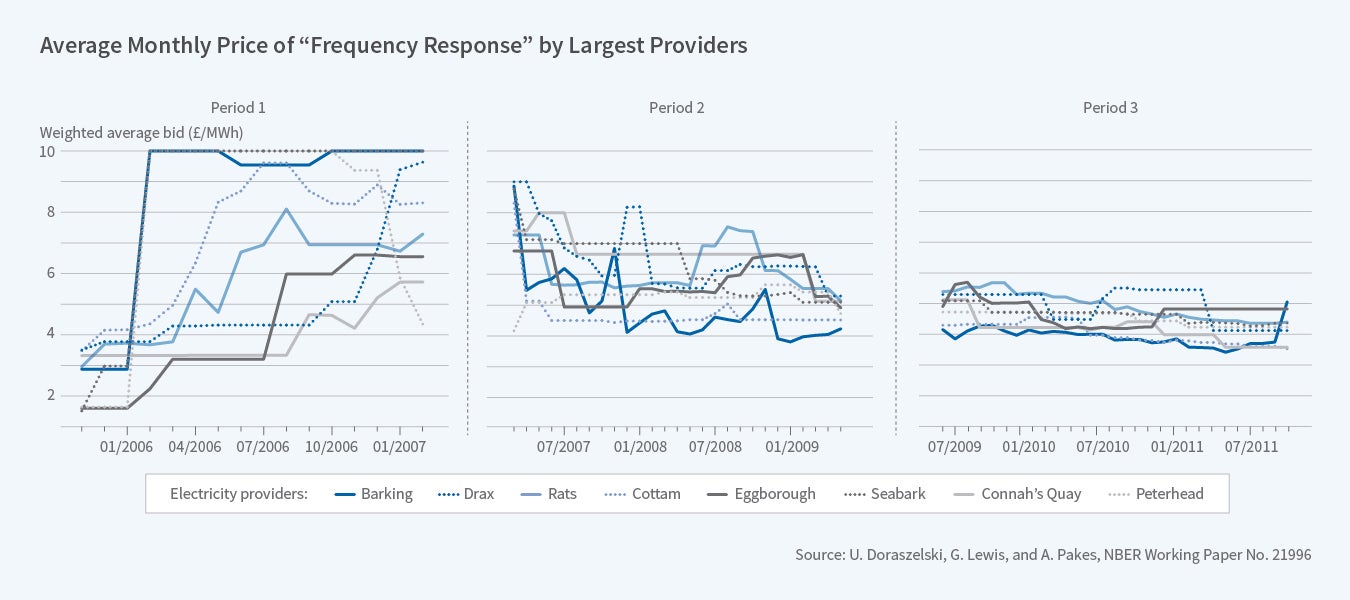
Figure 2 provides the sample paths of the bids of the eight largest firms in each period.
The timing and extent of price increases in the first period varied over firms generating extensive interfirm bid variance. Drax, a firm whose generators are favored by National Grid and which eventually earns the most revenues, has bids that increase only after it hires a person to manage the bidding process. The first period was also the only period in which there was any noticeable within-station variance in bids. Within-station variance is likely an indication of experimenting, as there is no within-station variance in either generator type or access to the grid.
At the beginning of the second period, Seabank and Barking decrease their bids and steal significant market share from Drax. This is followed by a series of price cuts by firms with high bids. In late 2007, Drax increases its bids significantly, holds its bids at the higher value for exactly two periods, and when it sees that its competitors do not follow it upward, heads back down. There were similar attempts by others later on. By the end of this period the inter-firm variance in bids had decreased dramatically. In the third period there was very little variance in bids either across firms, or within firms over time, and this despite the fact that this was the period in which market conditions changed most noticeably.
We did not know of a useable interacting agent model that allowed for experimentation and the extreme differences in behavior we observe in the first period, so we focused our analysis on the second and third periods. The analysis is based on agents' perceptions of the profits they were likely to earn from different bids. We assume they know the costs of supplying FR — largely the wear and tear on machines — from the pre-deregulation period, and estimate it assuming agents do not err on average in the third period, after the bids have settled down. These estimates were consistent with prior information on costs. We also estimated actual demand using a logit model with firm and time-specific fixed effects, data on the position of the firm in the main market, and bids.
The cost and demand parameters enabled us to compute an upper bound to lost profits by assuming each firm had full knowledge of both its competitors' bids and the demand parameters. The difference between the upper bound and the actual profits averaged only 3.5 percent. This may explain the slow adjustment process. As George Akerlof and Janet Yellen recognized, and Figure 1 illustrates, even small departures from optimal behavior may lead to aggregate behavior that is quite different from equilibrium.7
Given costs, all that is needed in order to formulate a bid are perceptions of the parameters of demand and perceptions of their competitors' behavior. To analyze beliefs about competitors' play, we assume that firms believe their competitors' play will be a random draw from the vector of their past plays, with the weight given to prior months' bids declining geometrically in a parameter we estimate. To analyze beliefs about demand parameters, we focus on adaptive learning models. In adaptive learning, the beliefs about parameters are obtained from an econometric analysis of the data available to agents when they form their bids. Throughout we compare the predictions from the learning models to each other and to the predictions obtained from a Nash equilibrium. The comparisons are made both in terms of mean square prediction error and in terms of predicting the cost of FR to National Grid.
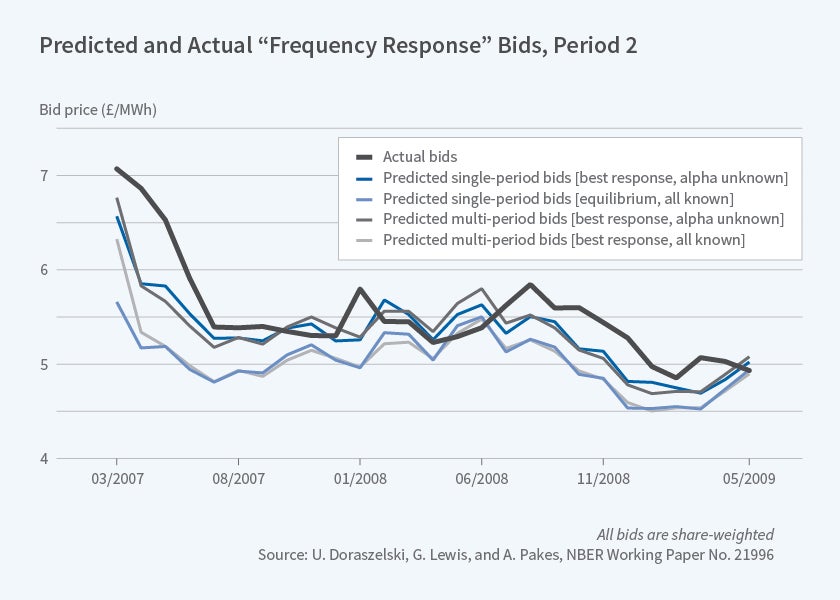
All measures of fit indicated that in the second period, the model that did best was one that used a fictitious play parameter that weighted more recent past play more than distant past play combined with an adaptive learning model that only needed to learn about the price coefficient. The difference between these models and the equilibrium model was both economically and statistically significant. It is easy to see why by looking at Figure 3. Only changes in cost and demand conditions affect the equilibrium predictions, and in the early periods they are small, so the equilibrium predictions go almost directly to the predictions of the learning models at the end of the period. In contrast, the model's prediction falls much more slowly and so do the actual bids. By the end of the second period, the equilibrium is close to our best model predictions.
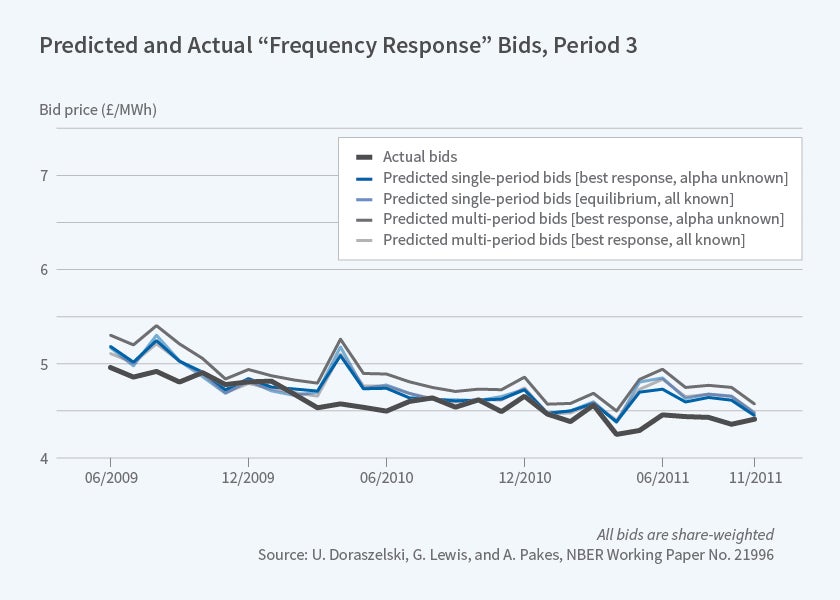
Comparison of predicted costs for the third period tells a very different story. [See Figure 4]. Now the Nash equilibrium and the learning models seem to mimic one another and both are much closer to the actual data. Relatedly, the mean square error of the bid prediction is one-third of the value in the second period. Recall that this is the only period with extensive environmental change post-deregulation.
We conclude that after changes large enough to cause a reevaluation of both the demand parameters and likely competitor play, the learning models generated by our theory and macro colleagues provided a better explanation of behavior than did Nash equilibrium. The fit of these models was not perfect, and there were attempts at more coordinated behavior, but these attempts were not successful. On the other hand, once the participants gathered sufficient information on the demand response to price and competitors' behavior, they seemed to be able to react to changes in a way that was very similar to what the Nash equilibrium predicted, albeit with a short lag.
Endnotes
S. Berry, J. Levinsohn, and A. Pakes, "Automobile Prices in Market Equilibrium: Part I and II," NBER Working Paper 4264, January 1993, and published as "Automobile Prices in Market Equilibrium," Econometrica, 1995, 63(4), pp. 841–90; S. Berry, J. Levinsohn, and A. Pakes, "Differentiated Products Demand Systems from a Combination of Micro and Macro Data: The New Car Market," NBER Working Paper 6481, March 1998, and Journal of Political Economy, 2004, 112(1), pp. 68–105.
G. S. Olley and A. Pakes, "The Dynamics of Productivity in the Telecommunications Equipment Industry," NBER Working Paper 3977, January 1992; and Econometrica, 1996, 64(6), pp. 1263–97.
R. Ericson and A. Pakes, "Markov-Perfect Industry Dynamics: A Framework for Empirical Work," Review of Economic Studies, 1995, 62(1), pp. 53–82.
A. Pakes, "Methodological Issues in Analyzing Market Dynamics," NBER Working Paper 21999, February 2016.
C. Fershtman and A. Pakes, "Dynamic Games with Asymmetric Information: A Framework for Empirical Work," Quarterly Journal of Economics, 2012, 127(4), pp. 1611–61.
U. Doraszelski, G. Lewis, and A. Pakes, "Just Starting Out: Learning and Equilibrium in a New Market," NBER Working Paper 21996, February 2016.